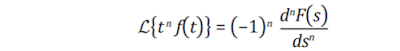UNIVERSIDAD LAICA "ELOY ALFARO" DE MANABI
FACULTAD DE INGENIERIA INDUSTRIAL
INTEGRANTES:
- CEDEÑO CHAVEZ MARLON ANTONIO
- GARCIA ALVIA LUIS FERNANDO
- PINCAY VIVAR RENSO WLADIMIR
TRANSFORMADA DE LAPLACE.
E
Definición.
- Dada f: [0, +∞] → C, se define formalmente la transformada de Laplace de f como la función de variable compleja:
- Sea f(t) una función continua en [0, ∞]. La transformada de Laplace de f(t) es la función f(s) definida mediante la integral:
El dominio de la función L(f) es el conjunto de números complejos z para los que la integral anterior es convergente. Dicho conjunto se denomina dominio de la transformada de Laplace y lo denotaremos por D (L(f)). Evidentemente, se dice que f es transformable Laplace si D (L(f))≠ ∅.
Es importante averiguar qué funciones tienen transformada de Laplace, es decir, hemos de dar un criterio sencillo de comprobar que nos permita saber si una determinada función tiene transformada de Laplace o si no la tiene. Para este fin daremos, en primer lugar, la siguiente definición:
Sea γ ∈ R. Se dice que la función f : [0, +∞[ → C tiene crecimiento exponencial de orden γ en infinito si existe una constante M > 0 de modo que:
Denotaremos por
Eγ al conjunto de las funciones f : [0, +∞[ → C que son continuas a trozos y
con crecimiento exponencial de orden γ en infinito. Por continua a trozos
entenderemos que en cada intervalo compacto [0, b] , con b > 0, f es
continua salvo a la suma en un número finito de puntos, y además las
discontinuidades en dichos puntos son de salto finito.
El resultado que sigue nos proporciona
un criterio sencillo de comprobar y que nos permite averiguar qué funciones son
transformables Laplace:
Modelo matemático.
La idea básica del uso de las transformadas integrales consiste en lo siguiente: supongamos que estamos estudiando un determinado fenómeno físico que describimos por medio de un modelo matemático. Dicho modelo estará formado por una o varias ecuaciones diferenciales (ordinarias o en derivadas parciales) con sus correspondientes condiciones iniciales y/o de contorno. El problema consiste en resolver dicho modelo matemático, es decir, resolver una ecuación diferencial. Es ahora cuando intervienen las transformadas integrales, en particular la transformada de Laplace, para transformar dicha ecuación diferencial en otra ecuación (algebraica o también diferencial), la cual va a resultar más fácil de resolver que la ecuación diferencial de partida. De esta forma transformamos nuestro problema original complicado en un problema más sencillo. Resolvemos el problema transformado y luego calculamos la transformada inversa de la solución del problema transformado con la esperanza, claro está, de que esta solución inversamente transformada sea la solución de nuestro problema original. En bastantes casos, esta esperanza se convierte en realidad y conseguimos, por este procedimiento, resolver nuestro problema original. Esquemáticamente, lo que estamos diciendo se puede resumir en algo así como:
PROPIEDADES DE LA TRANFORMADA DE LAPLACE
- Propiedad de linealidad de la transformada de Laplace
2. Propiedad de traslación en s : Nos indica cuando el proceso tiene un retraso en el tiempo.
Si la transformada de Laplace L{f(t)}=F(s) existe para s>α entonces:
- Demostración: De la definición se sabe que:
la cual es válida para s > a.
3.- Transformada de Laplace de la derivada
La transformada de la derivada primera de una función es igual a la transformada de la función sin derivar multiplicad por s, menos el valor de la función sin derivar para t=0:
4.-Propiedad de multiplicación por
Sea una función f(t) seccionalmente continua y diferenciable en el intervalo [0, ∞] ; entonces su trasformada de Laplace es también diferenciable y por lo tanto,
La demostración de este teorema es muy sencilla, bastará con derivar la función F(s) usando la definición de la transformada de Laplace e intercambiando el orden de integración y derivación.
5.-TRANSFORMADA DE LA INTEGRAL
4.-Propiedad de multiplicación por
Sea una función f(t) seccionalmente continua y diferenciable en el intervalo [0, ∞] ; entonces su trasformada de Laplace es también diferenciable y por lo tanto,
La demostración de este teorema es muy sencilla, bastará con derivar la función F(s) usando la definición de la transformada de Laplace e intercambiando el orden de integración y derivación.
5.-TRANSFORMADA DE LA INTEGRAL
La transformada de la integral de una función es igual a la transformada de la función dividida por s más el valor acumulado por la integral para t=0, también dividida por s:
Se puede demostrar aplicando la trasformada de la derivada, ecuación , considerando que f (t)] es la integral de f’(t) y cambiando la nomenclatura por el orden superior de integración.
6.-Propiedad de escalamiento en el tiempo
Una función está escalada en el tiempo y está definida por f(αt) de tal manera que su transformada
7.- Teorema del valor inicial : Nos indica las condiciones iniciales.
Sea f(t) una función seccionalmente continúa en el intervalo [0, ∞] , y cuya transformada F(t) existe. Entonces podemos conocer su condición inicial en t = 0 mediante la propiedad:
8.- Teorema del valor final: Nos indica el valor en el cual se estabilizará la respuesta.
Sea una f(t) función seccionalmente continúa en el intervalo [0, ∞] con transformada F(s) . Entonces podemos conocer f(∞) por la relación:
9.- Teorema de integración real
Si f (t) es de orden exponencial, entonces existe la transformada de f (t) y esta dada por
APLICACIÓN:
Una herramienta comúnmente usada en el diseño de control clásico es la transformada de Laplace, ya que en el estudio de los procesos es necesario considerar modelos dinámicos, es decir, modelos de comportamiento variable respecto al tiempo, esto trae como consecuencia el uso de ecuaciones diferenciales respecto al tiempo para representar matemáticamente el comportamiento de un proceso.
Para poder diseñar un sistema de control automático, se requiere:
- Conocer el proceso que se desea controlar, es decir, conocer la ecuación diferencial que describe su comportamiento, utilizando las leyes físicas, químicas o eléctricas
- A la ecuación diferencial se le llama modelo del proceso
- Una vez que se obtiene el modelo, se diseña el controlador
EJEMPLO DE APLICACIÓN
Se tiene un proceso como el mostrado en la figura. el flujo de entrada cambio repentinamente de 5m3/min a 15m3/min
cual es la altura final del tanque una ves que alcanzo la estabilización
Por que es importante controlar un proceso?
- Incrementa la productividad
- Seguridad
- Mejorar la calidad
- Reducir el tiempo de manufactura
- Certificación en mercados internacionales
Por que usamos la transformada laplace?
- Es necesario considerar modelos dinámicos (comportamientos variables respecto al tiempo).
Esto tiene como efecto el uso de ecuaciones diferenciales con respecto al tiempo.
- La trasformada laplace permite resolver ecuaciones diferenciales lineales mediante latransformación en ecuaciones algebraicas.
- Cuando ya estudiamos el comportamiento podemos diseñar y analizar los sistemas de control.
WEBGRAFIA.
http://lcr.uns.edu.ar/fvc/NotasDeAplicacion/FVC-Marianela%20De%20Benedictis.pdf